Faster JavaScript Memoization For Improved Application Performance

Whilst not new by any means, memoization is a useful optimization technique for caching the results of function calls such that lengthy lookups or expensive recursive computations can be minimized where possible.

The basic idea is that if you can detect an operation has already been previously completed for a specific set of input values, the stored result can instead be returned instead of repeating the operation again.

Some of the problems memoization can help optimize include: recursive mathematics, algorithmic caching of canvas animation and more generally, any problems which can be expressed as a set of calls to the same function with a combination of argument values that repeat.

A Brief History

If you're a history buff, you may be interested to know that the term 'memoization' was first coined in 1968 by a scientist involved in researching artificial intelligence named Donald Michie - it's based on the latin for the word memorable (memorandum). Michie proposed using memoized functions to improve the performance of machine learning and it's become more popular in recent years with the rise of functional languages such as Haskell and Erlang.

There's a plethora of excellent material that's been previously written about memoization and for further reading I recommend these pieces by John Hann and Nicholas Zakas. Douglas Crockford also briefly touched upon memoization in JavaScript: The Good Parts as does Stoyan Stefanov in JavaScript patterns.

Implementing Memoization - The Basics

Memoization is a concept that pre-dates the JavaScript programming language, but we can simply think of it as remembering the results for inputs of a specific value to a function.

When we say 'remember', we mean utilizing a form of cache to store a record of the computed output of such specific inputs so that if a particular function is subsequently re-queried with the same input, the remembered result is returned rather than a recalculation being necessary. A lot of the time, a simple array is employed for the cache table, but a hash or map could be just as easily used.

In most of the JavaScript implementations for memoization that I've reviewed, the memoization of a function (with a set of arguments) is conducted within an inner returned function whilst a signature or hash is employed for indexing the stored result.

One of the more easily readable memoization implementations can be seen below. This one is by zepto.js author, Thomas Fuchs. Whilst I prefer for memoization to be kept as a utility outside of the function prototype, this implementation does do a great job of clearly demonstrating the core concepts.

Function.prototype.memoize = function(){
    var self = this, cache = {};
    return function( arg ){
      if(arg in cache) {
        console.log('Cache hit for '+arg);
        return cache[arg];
      } else {
        console.log('Cache miss for '+arg);
        return cache[arg] = self( arg );
      }
    }
  }

// a hypothetical usage example

// imagine having a function, fooBar, as follows
function fooBar(a){ ... }
// once a memoizer is available, usage is as simple as
// applying it to our function as follows:
var memoFooBar = fooBar.memoize();
// note in other implems, this would probably be
// memoize(fooBar);
// we now use memFooBar for all calls to the original
// function, which will now go through the memoizer instead.
memoFooBar(1);
// the above call isn't cached, so any computations necessary
// are conducted. This result is then cached for next time.
memoFooBar(1); // will now return the cached result
memoFooBar(2); // whilst this will need to be calculated

The approach taken to actually caching results varies more greatly. The majority of developers prefer to maintain the cache outside of the returned function whilst others (Stoyan does this too) actually add custom properties directly to the function to be memoized.

With respect to the latter, it's considered best practice by developers such as Hann to avoid interfering with a user's code where possible. If a property cache is assigned to the function instance under a particular name, one limits the code calling your memoizer from using a similarly named property on the same instance. Whilst there may be a slim chance of this overlap actually occurring, this is just something to be aware of.

That said, I spent some time this week comparing a number of different memoization implementations and you may be interested to find out how a version that does hang it's cache on a user's function performs compared to those that keep it separate.

A Faster Implementation?

Just for fun, I put together a derivative implementation of memoization based on some prior work by @philogb, which should work fine for most trivial problems.

Some of the specific improvements I made include adding object argument testing and switching out the typeof check suggested in his post comments for determining whether or not to serialize arguments passed as objects into JSON text to use the more reliable Object.prototype.toString.call(). This update also consequently covers JSON stringifying arguments that are objeccts. For more information on this, feel free to read my post from a few weeks ago covering it.

Update: Mathias Bynens and Dmitry Baranovsky have provided some further optimizations to the implementation, which I've updated most tests to now also use.

Beyond this, much of the code is self-explanatory. args is a version of the function arguments that have been coerced into a JavaScript array, hash is handling serialization as covered above, fn.memoize is our cache and the final return is performing the cache lookup, storing the result of a particular set of input values if not already present.

/*
* memoize.js
* by @philogb and @addyosmani
* with further optimizations by @mathias
* and @DmitryBaranovsk
* perf tests: http://bit.ly/q3zpG3
* Released under an MIT license.
*/
function memoize( fn ) {
    return function () {
        var args = Array.prototype.slice.call(arguments),
            hash = "",
            i = args.length;
        currentArg = null;
        while (i--) {
            currentArg = args[i];
            hash += (currentArg === Object(currentArg)) ?
            JSON.stringify(currentArg) : currentArg;
            fn.memoize || (fn.memoize = {});
        }
        return (hash in fn.memoize) ? fn.memoize[hash] :
        fn.memoize[hash] = fn.apply(this, args);
    };
}

Now you'll notice that this implementation is making use of custom function properties, which I've previously said should be avoided if possible. So, why have I opted to show you this implementation instead of re-writing it to follow best practices?

Well, I collected together what I considered were some of the more robust memoization implementations I could find (including two from Fuchs and Hann) and when I benchmarked them on jsPerf using a common memoization problem, the above code (interestingly) outperformed the others by a respectable factor.

I was very surprised by this myself and double-checked the tests, had others review them and tested the output, but it would at the moment appear that this is one of the better memoization implementations available.

Now, I say *appear* as although the jsPerf test results favor this solution, my own offline tests conclude that at least 2 of the other implementations almost match it in performance.

Let us now review how memoization can be applied to optimizing a problem.

Benchmarking

The Fibonacci Series

Conventionally, many of the implementations of memoization you'll find have used the well-known Fibonacci series to demonstrate how it can help with recursive solutions to problems.

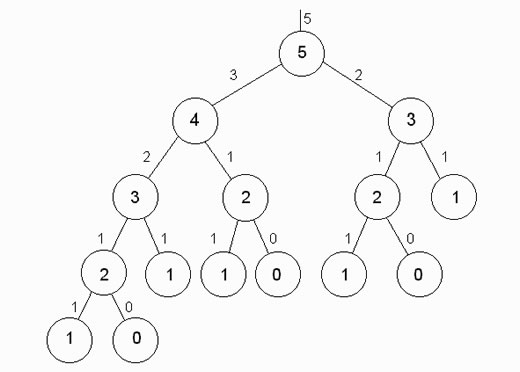
In case you're a little rusty on your high-school math, the Fibonacci series looks a little like this: 1,1,2,3,5,8,13,21,34.. etc.

Here, each number after the second, is the sum of the two numbers that appeared before it. Eg. 3 (let's call this 'x') = x-1 (ie. 2) + x-2 (ie. 1). A classic fibonacci problem might therefore be to discover what the 20th number in the series is.

Below you can see an implementation of a base function for calculating Fibonacci numbers that relies on recursion in order to generate the correct result.
 

function fib( x ) {
    if(x < 2) return 1; else return fib(x-1) + fib(x-2);
}

/*console profiling test*/
var fibTest = memoize(fib);
//first call
console.time("non-memoized call");
console.log(fibTest(20)); //varies (eg.10946)
console.timeEnd("non-memoized call");

//let's see how much better memoization fares..
console.time("memoized call");
console.log(fibTest(20));
//0ms in most cases (if already cached)
console.timeEnd("memoized call");

jsPerf Testing

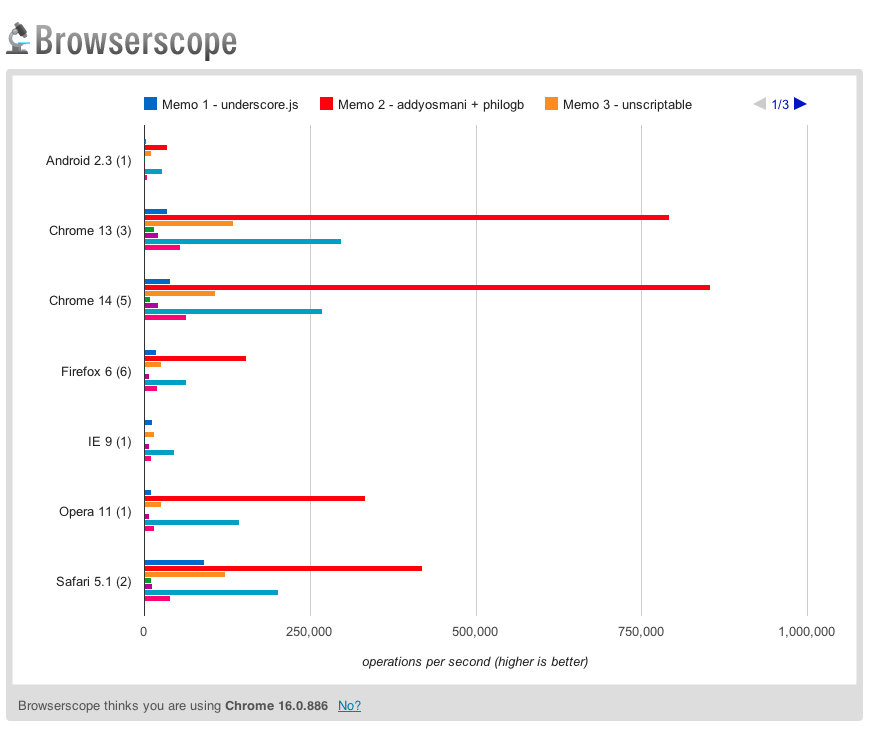
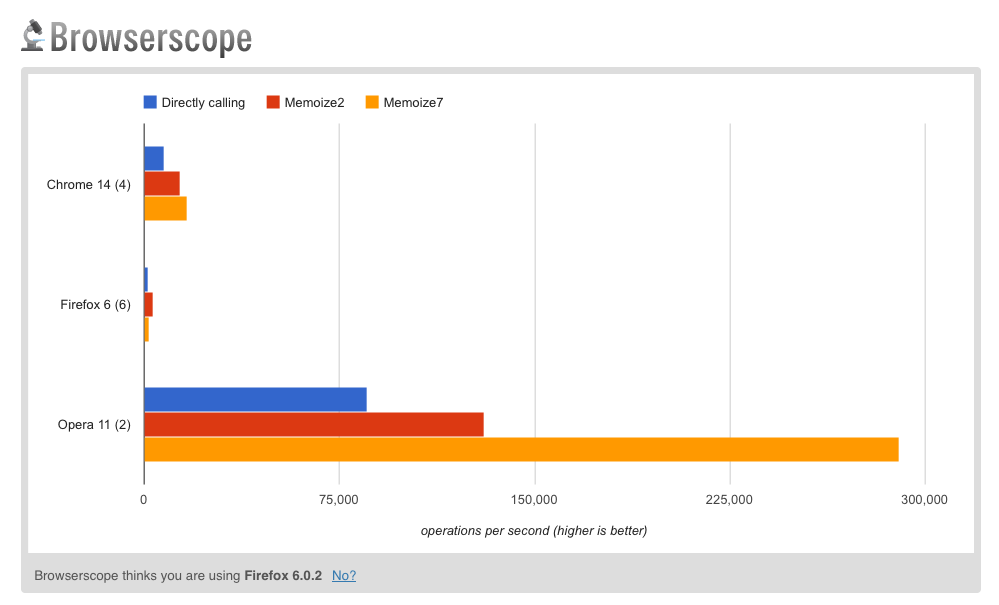
In the jsPerf test, a similar setup was used for comparing the performance of the implementation presented earlier with five others (including the memoization implementation found in Underscore.js). As you can see by the BrowserScope results listed, the performance difference (for this particular test) was favorable towards our implementation, particularly in Chrome and Firefox.

Note 1: If you're interested in comparing the performance of the actual cached value being accessed and used rather than just returned, tests for this can be found here (and also favor the newer implementation in many cases).

Note 2: Whilst not compared in this test, I previously benchmarked the effectiveness of all implementations vs. just calling fib(N) directly and the average improvement in lookup time was approximately 70%. Later in the post we'll take a look at this more closely.

If we continue working under the assumption that this is (for now) considered to be one of the more optimal approach to memoization in the tested set of implementations, the next obvious questions are why is this and is there anything better?.

Why is this faster?

I was genuinely curious as to why this particular implementation was being reported as performing better than the alternatives, so let's try exploring why.

Custom props on function instance vs. separate variables

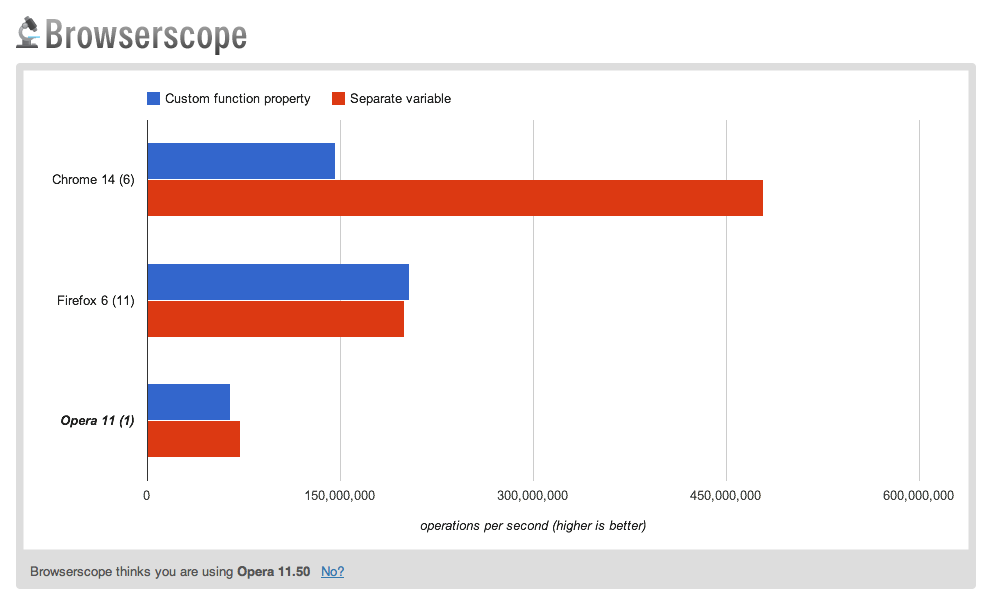
My initial theory was that maintaining the cache as a custom property on the function instance (as opposed to within a separate variable) may be resulting in more optimal property lookup times. If so, this would be interesting as I would have guessed that given both the instance and the external variable are objects, the difference in lookup times would be negligible. We can of course benchmark this theory just to see whether there is indeed a noticeable difference (jsPerf test here).

Curiously, in most browsers it would appear that the converse is in fact true. Using a separate variable performs more favorably in a simple property lookup test in both Chrome, Firefox and Opera.

Let's review the code once more

Reverting to @philogb's variation without the additional type checks, we can see that the bulk of the memoization logic lies in the final ternary expression being evaluated near the end of the returned function:

 function memoize( f ) {
  return function () {
      var args = Array.prototype.slice.call(arguments);

      //we've confirmed this isn't really influencing
      //speed positively
      f.memoize = f.memoize || {};

      //this is the section we're interested in
      return (args in f.memoize)? f.memo[args] :
                     f.memoize[args] = f.apply(this, args);
  };
}

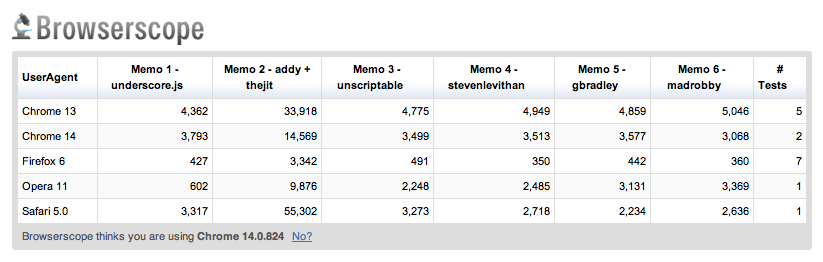
Whilst I won't be reproducing all of the implementations this is benchmarked against in this post, you're free to review them in the JavaScript prep section of this jsPerf test. One thing you'll notice is that the logic used for memoization itself is significantly more complex in many of the alternative solutions, with quite a few opting for additional conditional checks, in some cases unnecessarily.

To the best of my knowledge, this is the reason why this version performs better. It's simple and get's the job done.

Is there something that performs more optimally?

In my opinion, maintaining type-checking to determine the need for argument stringification is quite important. If however, you feel this is over-kill, a simpler solution that:

1. Does away with type-checking
2. Declares the function to be cached within the memoization implementation itself (as opposed to passing it in)
3. Only accepts one argument as opposed to many (which may work fine for some situations and should for our Fibonacci test)

is this version from Stoyan's 2009 JSConf talk:

  function memoize( param ){
      if (!memoize.cache) {
          memoize.cache = {};
      }
      if (!memoize.cache[param]) {
          var result = fib(param); //custom function
          memoize.cache[param] = result;
      }
      return memoize.cache[param];
  }

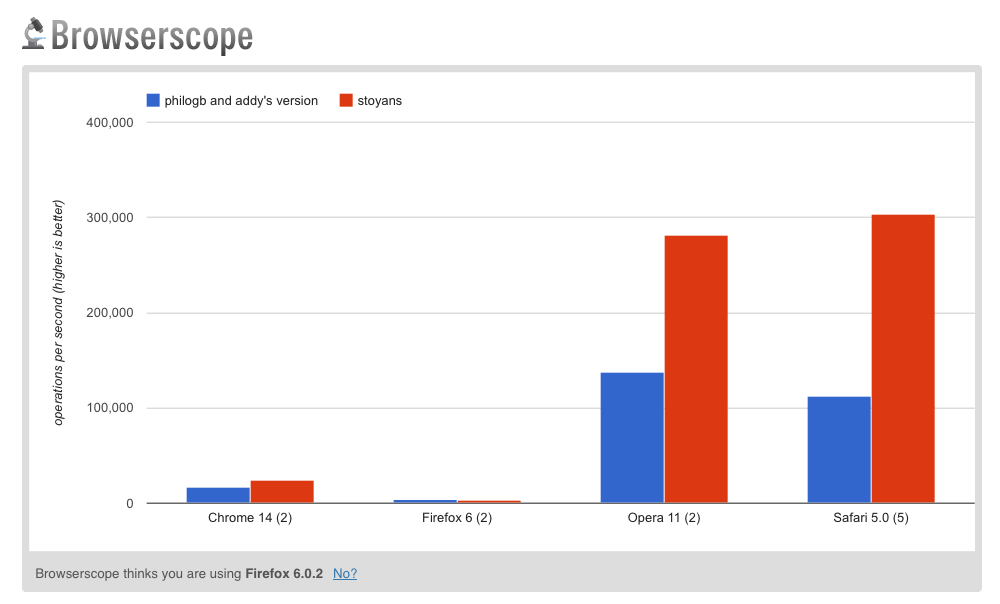
The jsPerf test comparing my version to the above can be found here. As you can see from the below results, Stoyan's implementation performs better in all browsers being tested as a result of these differences:

You may also be interested in taking a look at the tests comparing directly calling fib(N) in succession (blue) as opposed to using either our (Memoize2 - red) or Stoyan's (Memoize7 - orange) solutions:

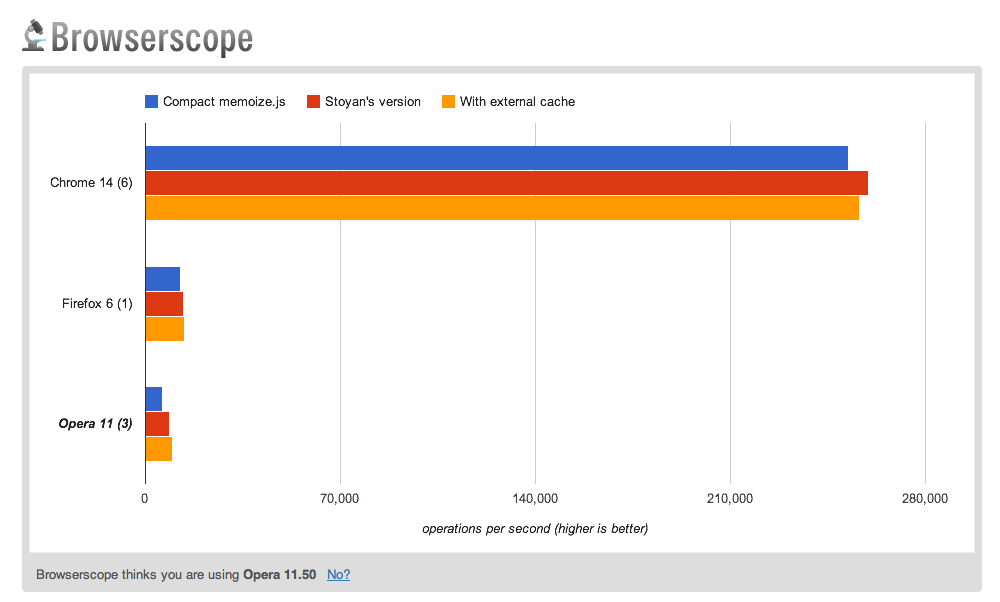
If a simple, compact implementation is what you're after, you may be interested in two variations of memoize.js that I've included below.

The first includes the minimal code required for memoization (cache + memoizer expression) using custom function properties. The second makes use of an external cache that is passed through to the memoizer, in case inline property definition isn't quite your thing.

In both cases, as you can see in the jsPerf comparison chart, a roughly equivalent level of performance is possible regardless of implementation. This leaves you free to select the implementation style you feel most comfortable with, but remember that these compact versions are only recommended for simple single-argument scenarios. For anything more complex, I recommend the complete implementation presented earlier.

// compact memoizer
function memoize1(param) {
   this.memoize = this.memoize || {};
   return (param in this.memoize) ?
   this.memoize[param] : this.memoize[param] = fib(param);
}

// usage: memoize1(25);


// using an external cache
var memCache = {};
function memoize2(param, cache) {
   cache = cache || {};
   return (param in cache) ? cache[param] :
   cache[param] = fib(param);
}

// usage: memoize2(25, memCache)


// stoyan's memoizer
function memoize3(param) {
   if (!memoize3.cache) {
       memoize3.cache = {};
   }
   if (!memoize3.cache[param]) {
       var result = fib(param); //custom function
       memoize3.cache[param] = result;
   }
   return memoize3.cache[param];
}

// usage: memoize3(25)

The jsPerf test for the below can be found here.

Practical Applications: Canvas

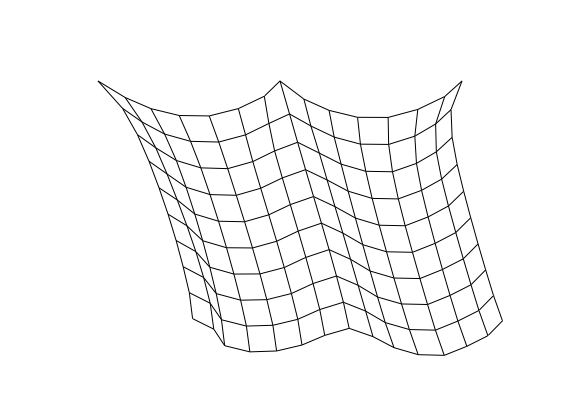
You'll often read about memoization being used to optimize complex algorithms, but they can also be used for visual applications with simpler routines such as those you might find in a lot of the Chrome canvas experiments.

Here's an example: Andrew Hoyer created an interactive canvas-based cloth simulation a while back that calculates reactionary point-data related to particular points in the cloth a user has clicked.

Every line in the cloth simulation is called a constraint and every point is a point mass (an object with no dimension, just location and mass). All the constraints do is control the distance between each point mass.

Rather than having to recalculate point-data if a user clicks on the same location twice, I've modified his demo to make use of memoization to cache calculations that have been previously made.

Clicking on a single point once caches the calculations for it, whilst clicking on it a second time (try double-clicking) will load from the memoized cache instead. A simple logger will let you know whether the cache has been hit or not lower down in the demo.

Memoization Pros

The benefits memoization has to offer are reduced (overall) execution time and potential improvements to overall performance, depending on what you're trying to achieve. It's particularly useful where you've detected levels of recursion in your application (eg. you're repeating the same computations as part of a larger operation or you're making some of the same repeated XHR calls regularly).

In general it works best when the result of passing a known set of parameters and values to a function will always result in the same value (eg. if the result returned by f(3,4) == f(3,4)). It can't however be applied to cases where f(3,4) != f(3,4). I've also personally found it quite helpful when working with recursive functions for drawing complex shapes (such as trees and fractals) to canvas, so it's utility does go beyond applications which may not be that visual or universally exciting.

Cons

With this in mind, memoization isn't appropriate if the method's output changes over time, is unlikely to be called again with the exact same set of parameters or is simplistic enough that there isn't much to be gained from using memoization as it comes with an overhead. A trivial, although silly, example of where memoization isn't appropriate is fetching stock market data as it regularly gets updated. Fetching a group of friends basic profile data however would make more sense with this technique as it's unlikely to change during a user's session.

Conclusions

Use of memoization generally needs to factor in what you're trying to do, the memory currently being consumed by recursive/iterative functions etc. You'll find that the more likely a task is to be repeated in your application, the greater potential memoization has for being of benefit. In closing, remember that memoization is both powerful, but also needs to be used carefully.

It can help cache the results of heavy queries quite well but this comes at the cost of of possibly storing large datasets (ie. you're trading speed for memory).